统一土的变形参数的实用本构模型

杨光华

（广东省水利水电科学研究院，广东省岩土工程技术研究中心）

2024.09.19

摘要：为解决土的复杂变形问题，提出了很多的本构模型用于表述土的变形特性。目前存在模型多，模型的参数多，不同的模型采用不同的参数，参数缺乏物理意义，缺乏统一的模型参数，工程应用难的问题。土的强度则统一用莫尔—库伦强度准则，统一用粘聚力c和内摩擦角φ表达土的强度参数，非常方便应用，使得工程中土的强度问题得到较好的解决，值得借鉴和参考。为此，土的变形问题也应采用统一本构模型，模型的参数采用统一的变形参数来表达，使不同的土的变形参数能具有可比性，才能更好的方便应用。为此，本文在广义位势理论基础上提出统一的弹塑性本构模型方程，模型参数可以统一用常规三轴试验获得的非线性切线模量E_t、泊松比μ_t来表达，这两个土的变形参数反映了土的非线性，压硬性、原状性的主要变形特点，既可用于弹塑性模型，也可用于非线性弹性模型。当假设应力应变曲线为双曲线时，非线性的切线模量E_t可用简单的变形参数来表征：土的初始切线模量值E₀，强度参数c、φ。这三个参数物理意义明确、易于确定，方便工程应用，可较好满足工程精度的要求，有望为工程提供一个统一的实用模型，破解工程应用的问题。

1 前言

土的强度和变形是土力学的两个基本问题，土的强度问题解决得较好，相对较成熟，主要原因是有一个公认统一的强度理论：莫尔—库仑强度理论，该理论所需的参数较少，就是黏聚力c和内摩擦角φ。虽然试验确定c、φ参数有时也难以准确，但由于参数少而简单，不同的土具有很好的可比性，随着应用时间的增长，积累的经验多，基本能判断c、φ值与土的物理性状的关系，因而有较好的把握确定c、φ的合理范围。

而土的变形，由于土是非线性的，变形特性复杂，通常是通过所谓的本构模型来表述，但目前模型众多，依据的理论也不统一，模型的参数多而不统一，尚未形成统一的模型、统一的模型参数，致使土的变形问题跟土的强度问题相比，远未成熟，模型多而难用。要解决土的变形问题，应要像土的强度问题那样，建立统一表达的模型，统一的参数，模型的参数能用方便确定物理意义明确的变形参数来表示，像土的强度参数c、φ那样便于应用，才能较好的破解本构模型难应用的问题。

2 土的变形特性及表征参数

要解决土的本构模型问题，参考土的强度问题的经验，应该是找到能较好表达土的变形特性的参数，然后统一用这个参数来建立本构模型，不断积累变形参数的经验值，方便应用。

土的主要变形特性可以用两个试验来确定，一是压缩试验，二是常规三轴试验。

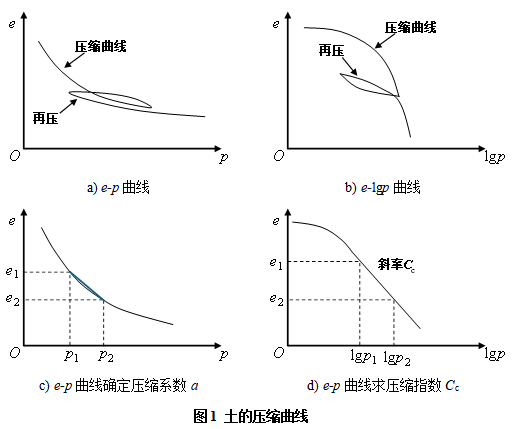
土力学教科书多数是把土的沉降变形看作为土体压缩所致，因此，对土进行一维压缩试验，获得其压缩变形曲线如图1a)、b)所示。

对正常固结土的压缩指数为一常数，对土是一个很好的指标，压缩指数由e-lgp曲线确定：

如图1d)所示。一般认为低压缩性的土C_c值小于0.2，高压缩性的土C_c值大于0.4，对认识土的压缩性是一个很好的指标。

土的另一个表示压缩性的指标是压缩模量E_s，由e-p曲线确定压缩系数：

如图1c)所示。土的压缩模量表示为侧限条件下的应力应变模量：.

通常工程中用p =0.1MPa~0.2MPa对应的压缩模量来表示土的压缩特性，记为E_s1-2，一般淤泥土的E_s1-2 =1.8~2.5MPa，淤泥质土的E_s1-2 =3~4MPa，这样的指标较易判断。但对于结构性土，压缩参数只能反映扰动后或重塑土的特性，对原状性土不能反映。

用压缩指数或压缩模量可以较好反映土的压缩性，已成为大家的共识，这是反映土体压缩性较好的指标，应用很方便。

但土的变形特性复杂，压缩特性不能全面反映土的变形特性，进一步的研究揭示土具有非线性（剪软性）、压硬性（围压影响）、弹塑性和原状性，常规三轴试验可以更好反映土的变形特性，通常不同围压下土的应力应变曲线如图2所示，由该曲线可以得到不同应用状态下土的非线性切线模量E_t和切线泊松比μ_t，可以较好的表征土的变形特性。

随着(σ₁-σ₃)增大，E_t变小，就是非线性（剪软性），E_t随着σ₃增大而增大，就是压硬性，邓肯—张模型假设曲线为双曲线方程时，得出E_t、μ_t的表达式为：

需要8个参数，μ_t <0.5为剪缩，μ_t >0.5为剪胀，因此，μ_t较好判断。

但对结构性土，存在取样扰动，室内试验较难反映现场原位土的真实特性，

杨光华提出可用现场原位压板试验确定土的初始切线模量E₀，这样（5）式的E_t可以改造为下式：

这样E_t就可以用E₀来表达了，E_t只需c、φ、E₀三个指标，方便了应用，E₀可以较好反映土的原状性，更准确可靠，为进一步反映压硬性。进一步又可增加一项改为：

则可以反映初始模量E₀的压硬性。

m一般可取为0.5已有较好的效果。对软土，E₀可用Es代替。

这样，用c、φ、E₀、m作为表征土变形的参数，有（9）式即可较好表述土的非线性、压硬性和原状性，主要是增加土的初始切线模量E₀，如果按双曲线假设，E₀ = 2E₅₀，E₅₀为土的变形模量，土的变形模量对于一些土可用标贯试验经验确定，如广东地基设计规范等，可近似大致取为

N—为标贯击数。

这样，如果我们假设土的非线性变形符合或接近双曲线方程，用双曲线模型可以较好的表述土的非线性变形特性，则土的变形特性可用c、φ、E₀、m这几个参数来表述，土的本构模型统一用这几个土的变形特性的参数来表达，则这样的模型就可方便于工程应用，具有较好的实用性，就像土的强度参数用指标c、φ那样方便，可以较好的解决土的变形问题。

3 理论模型和参数的统一

目前本构模型的现状是建立的模型不一致，依据的理论不同，所用的模型参数不同，这样不同模型难以比较，也较难积累模型参数的经验值和判断参数的合理性，难以使模型方便和可靠的应用。要破解这个问题，需参考土的强度问题，形成统一理论、统一模型，采用统一的简单易确定的变形参数来表达，这样才能破解模型应用性的问题。

以目前研究最多的弹塑性模型为例，建立模型需要屈服函数、塑性势函数和硬化参数，而不同模型有可能屈服函数、塑形势函数和硬化参数都不同，更难统一参数，不方便应用。其实如果从广义位势理论出发，最后的本构方程是与屈服函数、塑性势函数无关的，因此，要解决理论统一、模型统一应该从广义位势理论出发，则其弹塑性本构方程为^[1]：

其中，[De]为弹性矩阵。A、B、C、D四个参数为：

考虑弹性变形后，则为：

其实所有的弹塑性模型最后都归结为（12）式的弹塑性矩阵，而按广义位势理论的模型，模型只需要通过试验确定四个系数ABCD即可。而这4个系数，通过假设，可以进一步用前面的土的变形参数来表达。例如，假设满足传统的关联流动法则，则有

在常规三轴试验条件下，由式（15）式可得：

由(16)、（17）四个方程，即可以得到用E_t、μ_t和弹性体积模量Ke和弹性剪切模量Ge表示的ABCD四个系数：

则弹塑性本构方程即可确定。这样的模型只需用E_t、μ_t和弹性体积模量Ke和弹性剪切模量Ge这几个参数即可以。

比较剑桥模型和广义位势理论模型，也可以从剑桥模型中得到广义位势理论模型的参数。

比较（14）和（20）、（21）式可见，从剑桥模型或修正剑桥模型，也可以得到ABCD四个参数，从其他的弹塑性模型也可以得到ABCD四个参数。可见广义位势理论模型弹塑性矩阵具有统一性。

由前面可知，土的主要变形参数E_t可由E₀、c、φ、m这4个变形参数表达来确定，μ_t的变化不大，有时对变形影响不大时，可假设为一常数，这样我们只需这4个参数即可。对不同的土，这几个参数易于比较和方便确定，则应用就方便了。而参数中c、φ已在强度中解决，对非饱和硬土，通常m = 0.5左右即可有较好的效果，这样仅剩E₀，最好用现场原位压板试验确定，以解决室内试验对土样扰动的影响，或建立其他原位试验与E₀的经验关系，如用标贯试验、静力触探等，这样，就解决了土的原位性问题。

对于软土地基，则可以通过压缩试验确定的E_s来确定E₀。

这样像土的强度问题那样，我们采用足够精度的统一模型，形成统一的变形参数来确定本构模型的参数，而这些土的变形参数又能较方便可靠的确定，就可以提高模型计算的准确性和可靠性，推动本构模型的工程应用，最后可以像强度问题那样较好地解决土的变形问题。

结语

1. 土的强度问题解决得较好，主要是统一应用了莫尔—库仑强度准则，剩下的就是强度准则的两个参数黏聚力c和内摩擦角φ了，不同的土都用了相同的这两个指标来表征土的强度特征，这样不同的土就可以相互比较，甚至建立与土的物理指标的一定的关系，从可以较容易判断指标的合理性和可靠性，这就保证了强度计算的可靠性，使地基的强度设计理论与方法相对得到了较好的解决，这应该是解决土的变形问题值得学习和借鉴的地方。

2. 土的变形问题主要是通过本构模型来解决。但目前本构模型众多，模型参数多且不统一，有些参数也缺乏物理意义，不同的模型采用不同的参数，难以比较不同的土的参数的合理性和可靠性，也不易通过土的物理参数来辨识模型参数的合理性，工程中较难应用。这是影响本构模型工程应用很重要的原因。应该参考强度问题的解决方法，统一模型参数，用尽量少而物理意义明确的变形参数，才能积累不同土的参数的经验值，方便应用。

3. 广义位势理论模型是解决统一模型和参数的有效方法，从数学原理出发，假设清楚，可以统一应用常规三轴试验、三维压缩试验确定参数，可以考虑原状性，为统一土的变形参数提供了理论基础。在这一理论模型下，可以统一应用切线模量E_t、切线泊松比μ_t和压缩曲线的压缩模量E_s或压缩系数λ确定模型参数。当对土的应力应变曲线采用双曲线表述时，非线性切线模量E_t可以用几个简单的土的变形参数来表示：c、φ、E₀、m。这些参数物理意义明确，参数数量少，可以较易确定和比较不同土的参数，积累不同土的参数的经验值，提高参数的可靠性和方便应用。对一些简单问题，也可以假设泊松比μ_t为常数。这样的模型理论基础好，模型简单且有统一性，不同的土采用统一的变形参数，精度可以满足工程需求。由此可以形成方便工程应用的实用模型。这应该是破解土的本构模型应用，解决土的变形问题的有效途径。

4. 对于通常的工程问题，常规三轴试验和双曲线方程已足够反映土的主要变形特性，如非线性、压硬性，再考虑土的原状形，应该可以较好解决大部分工程的变形问题。如果认为双曲线方程不足以表述土的变形特性，也可以直接从试验曲线上得到不同应力状态的切线模量E_t、切线泊松比μ_t代入模型，则可以适应各种试验曲线。用E_t、μ_t于广义位势理论则可以建立弹塑性模型，用于广义虎克定律则可以建立非线性弹性模型，应用方便。

主要参考文献：

[1] 杨光华,李广信,介玉新著《土的本构模型的广义位势理论及其应用》[M]，北京：中国水利水电出版社，2007年

[2] 李广信 《高等土力学》[M]，北京：清华大学出版社，2002.[3] 杨光华，岩土类材料的多重势面弹塑性本构模型理论，岩土工程学报，1991年第5期。

[4] 杨光华，一个无需塑性势函数的新的土体弹塑性本构模型，《水工结构工程理论与应用》，大连海运学院出版社，1993年6月。

[5] 杨光华，李广信，岩土本构模型的数学基础与广义位势理论，岩土力学，2002年第5期。

[6] 杨光华，土的现代本构理论的发展与回顾展望，岩土工程学报，2018年第8期。